Στόχος και επιδιώξεις του ομίλου

1η ΣΥΝΕΔΡΙΑΣΗ: ΠΕΜΠΤΗ 19-10-2017

Συζήτηση για το στόχο και τις γενικές γραμμές του ομίλου.
Σε κάθε (δίωρη) συνεδρίαση θα γίνεται:
Α) ανάδειξη μαθηματικών εννοιών ως εργαλείων ερμηνείας και πρόβλεψης του κόσμου γύρω μας, με πειραματισμό πάνω σε πραγματικά προβλήματα. (1 ώρα)
Β) Παρουσίαση και ανάλυση μεγάλων μαθηματικών στιγμών της Ιστορίας των Μαθηματικών και προσπάθεια διασύνδεσης με τις υπόλοιπες επιστήμες και την Τέχνη. (1 ώρα).

Α) Διάκριση των φαινομένων σε α) Ντετερμινιστικά (αιτιοκρατικά - προβλέψιμα), β) Χαοτικά (ευαίσθητα στις αρχικές συνθήκες)  γ) Τυχαία. Παραδείγματα για κάθε περίπτωση. Μελέτη και ανάλυση ενός αιτιοκρατικού πειράματος.

Β) Μεγάλη στιγμή των Μαθηματικών: Οι τάξεις του απείρου. Ταξινόμηση των απειροσυνόλων- Ισοπληθικότητα φυσικών και αρτίων, φυσικών και περιττών, διαγώνιο επιχείρημα ισοπληθικότητας φυσικών και θετικών κλασμάτων, ισοπληθικότητα φυσικών και ακεραίων, φυσικών και ρητών. (Cantor).

Α)  « Η ΣΥΝΑΡΤΗΣΗ ΩΣ ΜΟΝΤΕΛΟ ΕΡΜΗΝΕΙΑΣ ΚΑΙ ΠΡΟΒΛΕΨΗΣ»

A1. Αναλύθηκε το έκθεμα - κατασκευή , η οποία αποτελείται από ένα παραλληλεπίπεδο το οποίο έχει δύο εισόδους και δύο εξόδους. Στο εσωτερικό του υπάρχουν τρεις τροχαλίες , οι οποίες ρυθμίζουν την κατεύθυνση του σφαιριδίου από την είσοδο στην έξοδο, αλλά δεν είναι εφικτή η πρόσβαση στο εσωτερικό της συσκευής.

Το ερώτημα που τίθεται είναι αν αφήνοντας ένα σφαιρίδιο από την ίδια είσοδο μπορεί να προβλεφθεί με ακρίβεια σε ποια έξοδο θα καταλήξει το σφαιρίδιο σε οποιαδήποτε τάξεως ρίψη. Το φαινόμενο είναι αιτιοκρατικό, δηλ. είναι δυνατή αυτή η πρόβλεψη;

Βήματα : Αρχίστε και παρατηρείτε προσεκτικά τις εκβάσεις του φαινομένου: Μπορείτε να καταγράψετε τις παρατηρήσεις σας;

Έχει κάποια σχέση ο αριθμός της ρίψης με την τελική έξοδο του σφαιριδίου;

Σε ποιους αριθμούς ρίψεων π.χ. το σφαιρίδιο εξέρχεται αριστερά (Α) και σε ποιους αριθμούς ρίψεων εξέρχεται δεξιά (Δ);.

Αν με f συμβολίσουμε τη διαδικασία μπορούμε να έχουμε την έκβαση του φαινομένου κατά την 243 ρίψη , δηλ. την f(243) ;

Μπορούμε να έχουμε την έκβαση του φαινομένου στη γενική του μορφή f(ν) όπου ν φυσικός αριθμός;

Δηλαδή ποια είναι η έκβαση του φαινομένου στην ρίψη με αριθμό ν;

Παρατηρώντας την καταγραφή διαφαίνεται ένα μοτίβο. Αν π.χ. επιλέξουμε την δεξιά είσοδο , συμβολίζοντας με Δ την δεξιά έξοδο και με Α την αριστερή έξοδο καταγράφονται τα εξής : Δ Α Δ Δ Δ Α Δ Δ Δ Α Δ Δ Δ Α Δ Δ Δ Α…

Από την καταγραφή προκύπτει ότι αν θεωρήσουμε ως αρχή το Α, αν το πλήθος των ρίψεων είναι ακέραιο πολλαπλάσιο του τέσσερα το σφαιρίδιο θα καταλήξει στην αριστερή έξοδο ενώ στις υπόλοιπες περιπτώσεις θα καταλήξει στην δεξιά έξοδο. Οι θέσεις είναι διακριτές κατά συνέπεια θα μπορούσαμε να τις συμβολίσουμε με Α, Δ1,  Δ2,  Δ3,

Στη συνέχεια δίνοντας τυχαίους αριθμούς ως προς το πλήθος ρίψεων και ζητώντας από τους μαθητές να «προβλέψουν» την έξοδο του σφαιριδίου , καταλήγουμε στον ζητούμενο αλγοριθμικό τύπο που δίνει την έξοδο του σφαιριδίου σε σχέση με το πλήθος ν των ρίψεων. Η αλγοριθμική διαίρεση του με το 4 δίνει αποτέλεσμα ν = 4 ∗κ + υ, με υ=0, 1, 2, 3 . Τότε η συνάρτηση έκβασης του φαινομένου στην ν ρίψη είναι F(ν) = υ, όπου υ=1=Α, υ=1=Δ1, υ=2=Δ2, υ=3=Δ3. .

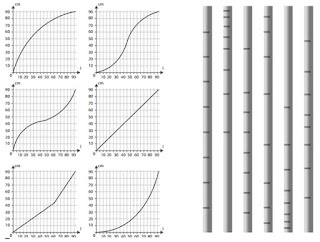
Τέλος ζητήθηκε η γραφική παράσταση της διαδικασίας, που είναι ένα περιοδικό μοτίβο, όντας περιγραφή ενός περιοδικού φαινομένου. 

A2. 

Β) Ορίστηκε το κριτήριο ισοπληθικότητας δύο συνόλων (1-1 αντιστοιχία των στοιχείων τους), και διαπιστώθηκε το παράδοξο οι φυσικοί αριθμοί να είναι ισοπληθικοί με ένα μέρος τους (τους αρτίους).  

Ο προφανής νόμος απεικόνισης είναι ότι σε κάθε φυσικό αριθμό n αντιστοιχίζεται μοναδικά ο άρτιος 2n. 

Εργασία : Μπορείτε να βρείτε το νόμο (συνάρτηση απεικόνισης των στοιχείων του Z με τα στοιχεία του Ν ;

Εργασία: 1) Μπορείτε να δικαιολογήσετε και να βρείτε το σχετικό νόμο αντιστοιχίας των περιττών με τους φυσικούς αριθμούς;   2) Μπορείτε να δικαιολογήσετε σχηματικά την 1-1 αντιστοιχία όλων των ρητών (θετικών και αρνητικών) με τους φυσικούς; 3) Αναζητείστε στο διαδίκτυο πληροφορίες για το μεγάλο μαθηματικό Cantor και το έργο του.