6η ΣΥΝΕΔΡΙΑΣΗ - ΠΕΜΠΤΗ 16-11-2017
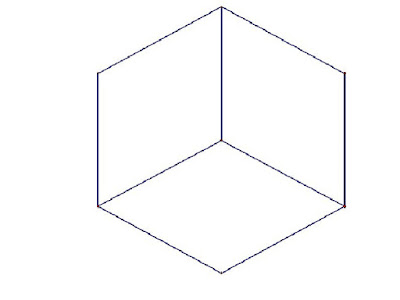
Στη σημερινή συνεδρίαση οι μαθητές του ομίλου εισήχθηκαν στην έννοια της ελαχιστοποίησης με ερέθισμα την σαπωνοειδή επιφάνεια που παράγεται από την παρακάτω κατασκευή :
Στη σημερινή συνεδρίαση οι μαθητές του ομίλου εισήχθηκαν στην έννοια της ελαχιστοποίησης με ερέθισμα την σαπωνοειδή επιφάνεια που παράγεται από την παρακάτω κατασκευή :
Το ερώτημα είναι γιατί η φύση επιλέγει αυτόν το σχηματισμό της σαπωνοειδούς επιφάνειας μεταξύ των τριών στύλων που συνδέουν τις δύο παράλληλες πλάκες.
Η πρώτη διαπίστωση μετά από κατάλληλους πειραματισμούς είναι ότι μια σαπωνοειδής επιφάνεια επιλέγει (για λόγους ελάχιστης ενέργειας) το σχηματισμό ελαχίστων μηκών και συνάμα επιφανειών.
Το πρόβλημα στην επίπεδη εκδοχή του διατυπώνεται μαθηματικά ως εξής : Υπάρχει και αν ναι, να βρεθεί σημείο Ο στο εσωτερικό τριγώνου ΑΒΓ ώστε το άθροισμα των αποστάσεων ΟΑ+ΟΒ+ΟΓ να είναι το ελάχιστο. (Η λύση του προβλήματος αυτού με απλή Ευκλείδεια Γεωμετρία πιστώνεται στο Μεγάλο μαθηματικό Fermat).
Οι αρχικές εικασίες των μαθητών ήσαν όπως είναι φυσιολογικό ότι ένα τέτοιο σημείο θα πρέπει να αναζητηθεί στα γνωστά "κέντρα" του τριγώνου (ορθόκεντρο, βαρύκεντρο, περίκεντρο κλπ).
Με τη βοήθεια του προγράμματος Sketchpad (που μπορείτε να κατεβάσετε και να εγκαταστήσετε από εδώ : ΠΡΟΓΡΑΜΜΑ SKETCHPAD ) απορρίφθηκαν οι εκδοχές αυτές.
Πειραματιστείτε και σεις μόνοι σας με τη βοήθεια του αρχείου (αφού έχετε πρώτα εγκαταστήσει το πρόγραμμα) :
Αφού διαπιστώθηκε ότι το ζητούμενο σημείο δεν έχει σχέση με τα γνωστά κέντρα του τριγώνου δόθηκε η λύση του Fermat, λύση που μπορείτε με περισσότερη ανάλυση του θέματος να δείτε εδώ :
Δείτε επίσης ένα βίντεο για τις σαπωνοειδείς επιφάνειες και τη σχέση τους με την αρχιτεκτονική της κυψέλης των μελισσών εδώ :
ώστε σε επόμενη συνεδρίαση να συζητήσουμε λεπτομερέστερα το όλο θέμα.
Επίσης προβληματιστείτε με το αντίστοιχο πρόβλημα για 4 σημεία, στο οποίο η φύση δίνει την λύση που δείχνει η επόμενη εικόνα, ώστε να το συζητήσουμε σε επόμενη συνάντησή μας:
Έχει σχέση το πρόβλημα των 4 σημείων και αν ναι ποια είναι αυτή, με το αντίστοιχο πρόβλημα των 3 σημείων;
Παρατήρηση : Δόθηκε στη διάρκεια της συζήτησης στους μαθητές για επεξεργασία και το κλασικό πρόβλημα ελαχιστοποίησης :
Σε ποια θέση του σημείου Μ το άθροισμα ΑΜ+ΜΒ γίνεται ελάχιστο. Η ορθή λύση υποδείχθηκε από μαθητή της Α Γυμνασίου!, (Κυριάκος) ενώ υπήρξε και η εξίσου σημαντική παρατήρηση μαθητή Γ Γυμνασίου, (Νίκος), ότι η ζητούμενη θέση του Μ έχει σχέση με το λόγο των αποστάσεων των Α και Β από την ευθεία!. Σημειωτέον ότι το πρόβλημα διδάσκεται σύμφωνα με το αναλυτικό πρόγραμμα σπουδών ως εφαρμογή-άσκηση στην Α Λυκείου!. Απόδειξη ότι οι γνωστικές-ερευνητικές δυνατότητες των μαθητών δεν περιχαρακώνονται σε ηλικιακά όρια.
Σημείωση: Η παρατήρηση του Νίκου (Γ Γυμνασίου) έγινε στο τέλος, κατά την αποχώρηση και δεν έγινε αντικείμενο ομαδικής συζήτησης. Θυμηθείτε να τη συζητήσουμε όλοι μαζί !